


János Bolyai is considered the greatest figure in Hungarian science who is thought to be the Copernicus of geometry. In his 26-page work published in 1831 and generally referred to as Appendix, which was an appendix to Vol. I of Tentamen, the two-volume monumental monograph of his father, Farkas Bolyai, he made a revolutionary achievement by the creation of the socalled non-Euclidean geometry. With this work János Bolyai broke the monopoly of Euclidean geometry and opened the way to think about space from another aspect. Through his findings in axiomatic thinking Bolyai formed the history of mathematics as a whole considerably. It can be claimed that the development of modern mathematics in the XIXth and XXth centuries can, to a large extent, be attributed to János Bolyai's discovery. However, the importance of his results became recognized only after his death but even then not without resistance. In his life his brilliant ideas, which had been matured at the age of 21, were not comprehended. He presented them with the brave revolutionism of the youth, having no fears for the criticism of the scientific establishment. Naturally, in this attitude there was a great degree of naivety, indeed, because he thought that great discoveries, including his ones, would lead to recognition and fame. But he who understood Bolyai's ideas, i.e., Gauss 'the prince of mathematicians' was unfair to János Bolyai when he formed his opinion on the Appendix in 1832. He said in his letter to Farkas Bolyai that he was unable to praise János's work because it would be as if he praised himself since the results in the Appendix and the way which had led to them coincided the thirty or thirty-five years' meditation of his almost literally. After Gauss's death in 1855 his bequest had been processed and no written proof of the aforementioned statement of his was found. In addition, a later conduct of Gauss is also reprehensible. When he obtained knowledge of the fact that the Russian Lobachevskii discovered the same, in essence, as János Bolyai did - he had the former elected foreign corresponding member of the Royal Society of Göttingen in 1842 - he failed to inform Lobachevskii that there was another person who had achieved similar results.
It has been stated long that although after his retirement in 1833 János Bolyai wrote a few things, including an important one on the foundation of complex numbers as well, the lack of recognition pushed him into a state of depression and, actually, he renounced creative mathematical research. It was Elemér Kiss, Professor at Marosvásárhely, who refuted this opinion: Having consulted Bolyai's manuscripts left to us for about a decade he found significant mathematical 'gems' in them which could be considered new at their birth.
*
20 years ago an article entitled 'Hyperbolic geometry: the first 150 years' was published by John Milnor the renowned mathematician of Princeton. He says in this article that non-Euclidean geometry had been in an uncertain state over its first 40 years. Later it integrated the more established branches of mathematics through Gauss's theory on curved surfaces and that of Riemann's on curved manifolds of higher dimension. Although it is true what Milnor says, reality is much more complicated than that.
The theory of the curvature and geometry of surfaces and manifolds of higher dimension did not lead out of mathematics, at least, not essentially. The interpretation of the curvature of surfaces and the study of their features could be placed into the existing system of mathematics. However, the case with Riemann's curved manifolds or geometry is different. In this theory a general approach to geometry appeared but only one quarter of a century later than the discoveries of Bolyai and Lobachevskii. Riemann discussed his theory in his habilitation paper in l854. By that time it began to be obvious what had not been at the time of the publication of Bolyai and that of Lobachevskii, i.e., geometry and reality may be different. Geometry may be conceived as a class of abstract theories, not giving up the intention of application, because its structures can arbitrarily be interpreted and studied just like functions or other mathematical objects. Incidentally, the paper was published after Riemann's death in l868.
Before the discovery of non-Euclidean geometry, the science of geometry was supposed to describe the real world around us, unseparable from it. Geometry was a kind of natural science. The point, the right line and the plane were what our imagination forcefully imposed on us. It should be remembered that the Euclidean axioms were born only for the sake of order in our thinking. They have been formulated in order that we should find our way in the chaos of concepts and statements and clarify what is evident and what is to be proven. Obvious statements and axioms should be the least numerous as much as possible. Statements which can be deduced from the others should not be regarded axioms.
Before the discovery of János Bolyai mathematicians expected a genius to come who would prove postulate V brilliantly, relying on other axioms. The immediate predecessors, Saccheri and Lambert, supposed this postulate to be untrue in order that they should arrive at a contradiction through indirect proof, for the world is Euclidean. They did not put it but thought like that. From the greatest philosopher of the age Immanuel Kant to the man of the street that was the conviction. Today, it is known that the teaching of the theory of relativity is different and there are experimental proofs of it but this fact, too, is known only by the more erudite. Our everyday lives and activities are based on Euclidean geometry. When a child draws lines in his copy-book, when a geometer surveys our land, he does not need to care whether more parallels may be drawn to a given right line through a point lying outside of it.
Bolyai sent geometry to the world of abstract theories. He showed that, logically, more than one geometries were also possible. As he said in his letter of 3 November 1823 sent from Temesvár to his father: 'From nothing I have created a new different world' - an abstract world, of course.
But if the world follows Euclidean geometry, what is the use of this at all? Gauss dared not publish his results in connection with non-Euclidean geometry which were partial results compared to those of Bolyai's; he dared not publish them either for fear that he would be thought mad. However, Bolyai was a revolutionary; he had the courage of his convictions. But for the sake of objectivity it also should be mentioned that Bolyai was convinced he would be understood and would receive the deserved recognition, based on his work.
After the letter of November 1823 Bolyai put down his results in German and gave his paper to Johann Wolter von Eckwehr his one-time professor in Vienna and supervisor in Arad in 1826. His father encouraged him to write his paper in Latin, too, which was published as an Appendix to the Tentamen, the two-volume monumental work of Farkas Bolyai. Its full title is as follows:Appendix, Scientiam Spatii absolute veram exhibens; a veritate aut falsitate Axiomatis XI. Euclidei (a priori haud unquam decidenda) independentem; adjecta ad casum falsitatis quadratura circuli geometrica. In English: Appendix, The absolute true Science of Space exhibited; independently of the XIth Euclidean Axiom (that can never be decided a priori) being true or false; for the case of being false the geometric quadrature of the circle is supplemented.
János Bolyai did not attempt to publish his work in any of the leading mathematical periodicals of his age. To this his father would have had connections with the help of Gauss but that thought had not been raised, perhaps, luckily for János, because as it is known Gauss wrote a letter to Farkas about the Appendix forwarded to him in 1831 which made János depressed. Although Gauss had a good opinion about the findings in the Appendix, he also said he had already discovered them. We have already cited some parts of this letter.
The Appendix was published in Hungarian and other languages several times. It was translated into English by George Bruce Halsted of Texas in 1891 which was issued, together with the translator's preface in the English translation of Bonola's book (l911) that had been written in Italian originally. Excluding the title page etc. the Appendix is a work of 24 pages. About this Professor Halsted says in his preface: 'These are the most extraordinary two dozen pages in the history of thinking'. Well, in addition to our laudation of János Bolyai, let us get acquainted with some of the characteristic results of his work.
As has been mentioned, Bolyai was still thinking within the system of the Euclidean axioms; the more complete axiomatic system of Hilbert was published in 1899. However, as far as his deduction in the Appendix and his methodology in general are concerned, Bolyai had utilized the great inventions of the former centuries, first and foremost, the analytical geometry of Descartes as well as the differential and integral calculus of Newton and Leibnitz. In a sense, the former meant to be a new and higher level of exactness, not only a solution of geometrical problems by the means of algebra.
Euclid’s Vth postulate can be stated as: given a line l and a point P lying outside the line in the plane, there exists exactly one line incident to P and parallel to l. This equivalent form of the Vth postulate is due to Playfair (1748-1819).
Bolyai first, rejecting postulate V (which bears the name axiom XI with him), defines parallelism. Consider a line l and a point P outside the line. If, starting from P, we draw a half line which intersects l in one direction, move the intersection into infinity, there will be a limiting position, where the line does not intersect l any more (see Figure 1). We can do the same in the other direction. If we continue both half lines into the other directions as well, then we obtain two lines both of which are parallel to l. If they are distinct, then there are infinitely many lines between the two which are also parallel to l but they have different properties. The geometry, corresponding to this case, is called hyperbolic.
At this point we remark that Bolyai’s lines are not lines in the everyday sense even though we visualize them as such on Figure 1. Lines in the Bolyai-Lobachevskii geometry may be half circles or other geometrical objects.
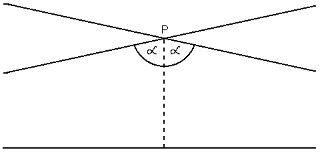
Figure
1
Parallel lines
Bolyai developed the absolute geometry that is independent of postulate V. The theorem stated below belongs to the absolute plane geometry. If a point P has distance d from line l and α is the angle between the line incident to P and orthogonal to l and the limiting position line parallel to l, then Bolyai’s formula holds:
![]()
Here k is a universal constant, independent of the choices of l and P.
Bolyai developed hyperbolic trigonometry and applied it to calculate surface and volume. For example, the circumference of the circle of radius r in hyperbolic geometry is given by
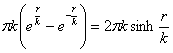 ,
,
where k is the already known universal constant. In later mathematical works this is identified with the reciprocal value of the curvature of the space. If k→∞, then as limiting value we obtain 2rπ which is the well-known formula for the circumference of the circle in Euclidean geometry.
One of Bolyai’s most beautiful theorems is the following. The sines of the angles of a triangle are in the same proportion to each other as the circumferences of the circles whose radii are equal to the sides opposite to the angles. If A, B, C designate the angles, a, b, c the sides and Οr the circumference of the cirle of radius r, then Bolyai’s theorem can be stated as:
![]() .
.
In Euclidean geometry
![]()
thus the above formula takes the form:
![]() .
.
On the other hand, in hyperbolic geometry we have
![]()
from which it follows that
![]() .
.
Now, consider two
parallel lines: a, b and take one point on each of them: A,
B. Earlier we mentioned that the lines have directions too, let M,
N designate them (see Figure 2). Assume that the angle MAB is
equal to the angle NBA. Then the points A, B are called
izogonal corresponding, or briefly corresponding, points (the term is due to
Gauss) and the fact is expressed by the relation A![]() B (notation of János Bolyai). This relation is independent of postulate
V, belongs to the realm of absolute geometry, and has the symmetry, reflexivity
and transitivity properties: A
B (notation of János Bolyai). This relation is independent of postulate
V, belongs to the realm of absolute geometry, and has the symmetry, reflexivity
and transitivity properties: A![]() A;
if A
A;
if A![]() B,
then B
B,
then B![]() A;
if A
A;
if A![]() B
and B
B
and B![]() C,
then A
C,
then A![]() C.
If a relation has the above properties, then it is called equivalence relation.
It is well-known that any equivalence relation in a set gives rise to a
subdivision of the set into disjoint subsets. These are called equivalence
classes.
C.
If a relation has the above properties, then it is called equivalence relation.
It is well-known that any equivalence relation in a set gives rise to a
subdivision of the set into disjoint subsets. These are called equivalence
classes.
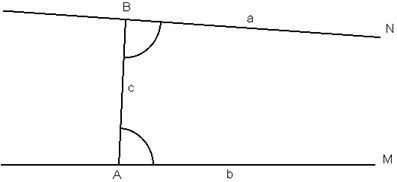
Figure 2
Corresponding points
Now, each equivalence class, produced by the correspondence relation, is a planar set in which – as Bolyai demonstrated it – the Euclidean geometry is valid. These are called horocycles.
Similar is the definition of the horosphere. In a horosphere too, the Euclidean geometry is valid. The horocycle, horosphere can be regarded as circle, sphere of infinite radius, respectively.
If the angles of a triangle are a, b, g, then in Euclidean geometry a+b+g=p, in hyperbolic geometry, however, a+b+g<p. The difference p-(a+b+g) is called the defect of the triangle. Bolyai proved that the surface D of the triangle is equal to the quantity:
![]()
where k is the universal constant. This formula was known to Lambert but Bolyai gave an exact proof to it.
One further interesting theorem of Bolyai is the following: for the legs a,b and hypotenuse c of a right triangle (angle between two lines means the one at the intersection of the lines) we have the formula:
![]() .
.
If k→∞, then, as limiting case, we obtain the formula c˛=a˛+b˛ which is Pythagoras’ theorem.
Farkas Bolyai, on a few pages in the Tentamen, made some remarks to the Appendix. Among them he gave a more detailed proof for the above limiting relation.
Finally, it should be mentioned that in the Appendix Bolyai is also concerned with constructions within hyperbolic geometry.
Other mathematical studies of János Bolyai are discussed in depth by the following authors: Pál Stäckel (1914), Lajos Dávid (1979), János Bolyai (Ferenc Kárteszi ed., 1977), Tibor Weszely (l98l) and Elemér Kiss (1999). Bolyai's impact on the development of geometry is discussed in the paper by Ottó Varga (1953). Milnor's already mentioned paper (1982) is the latest survey on the results in hyperbolic geometry. The annotated publication of the non-mathematical writings of János Bolyai is underway.
The other great discoverer of non-Euclidean geometry is the Russian Lobachevskii (1793-l856). The difference between the work of Bolyai and that of Lobachevskii may be summarized like this: while Bolyai elaborated absolute geometry, too, Lobachevskii provided a more detailed formulation of hyperbolic trigonometry. There is no reason for the debate over priority. In order that we should see something in this respect, the following can be mentioned.
Lobachevskii's first publications on non-Euclidean geometry were issued in Russian in Kazan Messenger in 1829-1830. Bolyai's Appendix was published as a reprint in 183l but the year of the imprimatur of the whole Tentamen is 1829. It is known that Bolyai elaborated his geometry in outlines in 1823 and the full German text was ready in 1826. Since the latter has been lost and the former is only a report of the discovery in a letter, there are no earlier written documents on Bolyai's discovery than the Appendix. On the other hand, it can also be said that Lobachevskii held a lecture on the relevant topic at the University of Kazan in 1826 but if the title of this is scrutinized, we may see that the lecturer intended to prove postulate V at that time (Elemér Kiss, l999).
According to some authors the geometry of Bolyai and Lobachevskii is the criticism of the Kantian conception of space; according to others it is a refutation of that. Their argumentation goes on like that: If in our mind there is room for both the Euclidean and the hyperbolic geometries, it is not possible that our concept on space is a priori in us, independently of our experiences about objects.
Undoubtedly, the absolutization of Euclidean geometry in Kantian philosophy proved to be a dead-end not so much because of the Bolyai and Lobachevskii geometry but the physical results of the twentieth century. However, the notion of Kant that space is Euclidean can be separated from the other notions of his concerning space which are subtler and different from the one which can be read in the aforesaid contrary opinion. Kant did not ignore that more than one abstract mathematical theories on space might also be formulated.
Still, in the age of Gauss, Bolyai and Lobachevskii Kantian philosophy was considered a definite supporter of Euclidean geometry. Unlike Gauss, who was afraid to publish his result because of the attacks of the Boeotians, who were regarded pleasure-seeking and stupid people by the Athenians, Bolyai and Lobachevskii did not fear to do so: both of them were revolutionaries. They revealed their scientific convictions to the world with courage.
References:
Benkő S. (1968). Bolyai János vallomásai. Irodalmi Könyvkiadó, Bukarest. Második kiadás: Kriterion Könyvkiadó, Bukarest, 1972.
Benkő S. (1978). Apa és fiú (Bolyai tanulmányok). Magvető Könyvkiadó, Budapest.
Bolyai Farkas (1832-1833). Tentamen juventutem studiosam in elementa matheseos purae, elementaris ac sublimioris, methodo intuitiva, evidentiaque huic propria, introducendi. Cum Appendice triplici. I.,II. Maros Vásárhely.
Bolyai Joannes (1831). Appendix, Scientiam Spatii absolute veram exhibens; a veritate aut falsitate axiomatis XI. Euclidei (a priori haud unquam decidenda) independentem; adjecta ad casum falsitatis quadratura circuli geometrica. Maros Vásárhely.
Bolyai levelek (1975). Válogatta, a bevezető tanulmányt írta és a jegyzeteket összeállította Benkő Samu. Kriterion Könyvkiadó, Bukarest.
Bolyai János (1977). Appendix, a tér tudománya (ed. Kárteszi Ferenc). Akadémiai Kiadó, Budapest.
Bonola, R. (1911). Non-Euclidean Geometry. Dover, New York.
Dávid L. (1979). A két Bolyai élete és munkássága. Második, bővített kiadás. Gondolat, Budapest.
Euklidész (1983). Elemek. Gondolat, Budapest.
Kiss E. (1999). Matematikai kincsek Bolyai János kéziratos hagyatékából. Akadémiai Kiadó, Budapest.
Lobacsevszkij, N. I. (1951). Geometriai vizsgálatok a párhuzamosok elméletének köréből (V.F. Kagan bevezetésével, magyarázataival és függelékével). Akadémiai Kiadó, Budapest.
Milnor, J. (1982). Hyperbolic geometry: The first 150 years. Bull. (New Series) Amer. Math. Soc. 6, 9-24.
Stäckel, P. (1914). Bolyai Farkas és Bolyai János geometriai vizsgálatai I-II. Budapest.
Varga O. (1953). A Bolyai-Lobacsevszkij geometria hatása a geometria fejlődésére. MTA Mat. Fiz. Tud. Oszt. Közl. 3, 151-171.
Weszely Tibor (1981). Bolyai János matematikai munkássága. Kriterion, Bukarest.
*
Reproducido a partir de:
Prékopa, András:
«The revolution of János Bolyai»,
pp. 3-59, en:
Non-Euclidean Geometries
János Bolyai Memorial Volume
Col.: Mathematics and Its Applications , vo. 581
Prékopa, András; Molnár, Emil (eds.)
Nueva York (N.Y.): Springer, 2006
2006, XIII, 506 p. 75 ilust., Tapa dura
ISBN: 978-0-387-29554-1
Con el permiso de Springer Science y Business Media.